크래프톤 정글에서의 1주차를 마치는 Week-I-Learn [2]
해당 글은 Notion TIL & WIL DB에서도 확인하실 수 있습니다.
2025.07.15
Brute-Force & Back Tracking
Brute-Force란
- 모든 경우의 수를 체크해서 정답을 찾는 방식
- e.g., 4자리 정수 비밀번호 탐색 시에
- 0000 ~ 9999까지 모든 경우의 수를 다 탐색하는 것
- 쉽게 보면, 반복문과 조건문 만으로 모든 경우를 만들어 답을 구하는 것
- e.g., 4자리 정수 비밀번호 탐색 시에
- 하지만, 일반적으로는 위와 같이 사용하는 경우는 매우 드묾
- 저명한 사실이지만, Time Complexity와 Space Complexity 를 고려하였을 때는 결코 좋은 선택지가 아니기 때문
- 때문에, 아래의 소개할 많은 알고리즘들을 대체해서 사용함
Bitmask
- 컴퓨터의 비트를 이용하여 집합을 표현하고 처리하는 기법
- 적은 메모리 공간에서 다양한 연산의 수행이 가능
Shifting연산a >> b: a의 모든 비트를 오른쪽으로 b만큼 이동a << b: a의 모든 비트를 왼쪽으로 b만큼 이동
num = 181 # 0b10110101
shift_num = num << 1
print(shift_num) # 362
print(bin(shift_num) # 0b101101010
num = 181 # 0b10110101
shift_num = num >> 1
print(shift_num) # 90
print(bin(shift_num)) # 0b1011010
AND연산 (&)- True
- 1 + 1
- False
- 1 + 0
- 0 + 1
- 0 + 0
- True
NOT연산 (~)- 1 → 0
- 0 → 1
OR연산 (|)- True
- 1 + 1
- 1 + 0
- 0 + 1
- False
- 0 + 0
- True
XOR연산 (^)- True
- 0 + 1
- 1 + 0
- False
- 1 + 1
- 0 + 0
- True
- 참고 자료
Permutation & Combination
- 순열(Permutation)
- 원소 개수가 r 개인 순열 뽑기 (중복 X, 순서 O)
from itertools import permutations
iter = [1, 2, 3, 4]
for i in permutations(iter, 2):
print(i)
# Output
# (1, 2), (1, 3), (1, 4), (2, 1), (2, 3), (2, 4), (3, 1), (3, 2), (3, 4), (4, 1), (4, 2), (4, 3)
- 조합(Combination) (중복 X, 순서 X)
- 원소 개수가 r개인 조합 뽑기
from itertools import combinations
iter = [1, 2, 3, 4]
for i in combination(iter, 2):
print(i)
# Output
# (1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (3, 4)
- 중복 순열
- 여러 iterable 요소들의 순서쌍을 반환하는 iterator 생성
from itertools import product
iter = [1,2,3,4]
for i in product(iter, repeat=2):
print(i)
# Output
# (1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4), (3, 1), (3, 2), (3, 3), (3, 4), (4, 1), (4, 2), (4, 3), (4, 4)
- 중복 조합(중복 O, 순서 X)
- iterable에서 원소 개수가 r개인 중복 조합 뽑기
from itertools import combinations_with_replacement
iter = [1,2,3,4]
for i in combinations_with_replacement(iter, 2):
print(i)
# Output
# (1, 1), (1, 2), (1, 3), (1, 4), (2, 2), (2, 3), (2, 4), (3, 3), (3, 4), (4, 4)
Back Tracking
- 퇴각 검색이라고도 함
- 한정 조건을 가진 문제를 해결하는 전략
- 구현
- 해를 얻을 때까지 모든 가능성을 시도
- 가능한 모든 내용을 하나의 트리로 구성하여 가지 중 해결책이 있고,
- 그 해결책을 찾아가는 전략
- 탐색 중 오답을 만난다면 이전의 탐색으로 돌아가는 기법
- 일반적으로 Recursion으로 구현
Back-Tracking을 가장 잘 표현하는 문제
3 x 3 행렬 선택 게임
- 아래표와 같은 3x3 행렬이 있을 때, 선택한 숫자들의 행과 열은 모두 중복하면 안됨
- 가장 작은 점수를 얻을 때 승리
| 1 | 3 | 5 |
| 2 | 4 | 7 |
| 5 | 3 | 5 |
- 알고리즘
- 먼저, 구조화를 진행
- 숫자 3개를 선택하여 직접 모두 다 해보는 것(Brute-Force)도 정답이 되지만,
- 더 효율이 좋은 방안을 찾기 위해서는
한정 조건을 탐색
-> 한정 조건 : “행과 열이 달라야 한다.” - 행렬 자체를 구조화하면,
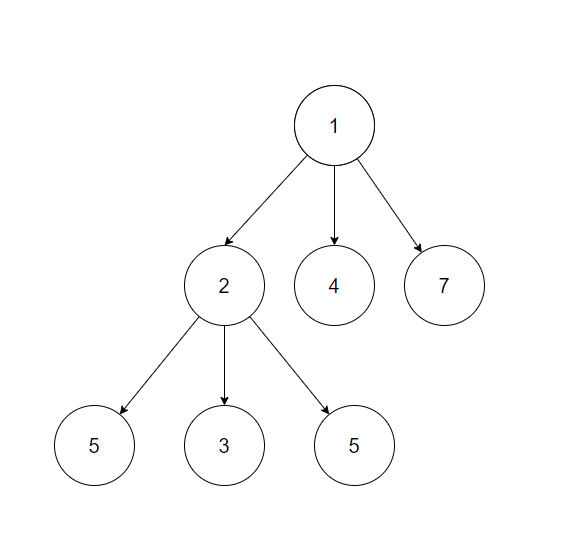
- 하지만, 한정 조건을 대입하여 구조화하면,
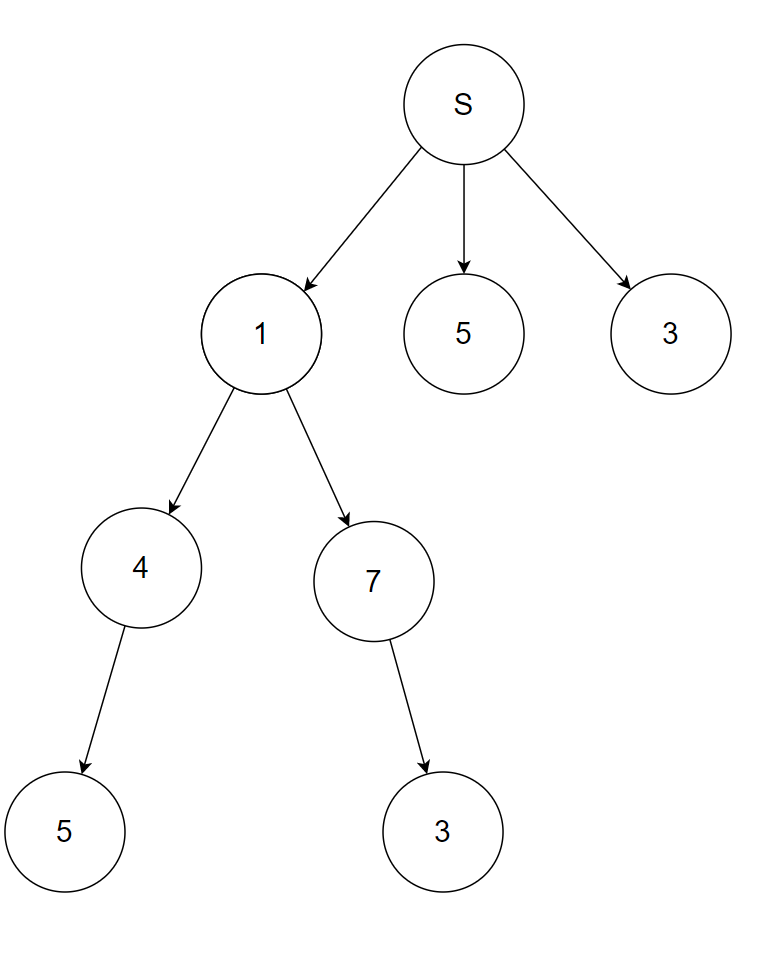
- 사진 출처 : 팔만코딩경
- 이러한 한정 조건을 적용한 후에, DFS를 통해 전체 탐색을 진행
- 이 때, 노드에는 유망한(정답이 될 가능성이 있는) 숫자만 추가
- 즉, 첫번째 행에서 1을 택한다면, 두번째 행의 숫자는 4, 7 둘만 노드에 추가
- 이 과정을 고도화 시키는 것.
- 먼저, 구조화를 진행
- Code
import sys
li = [[1, 5, 3], [2, 5, 7], [5, 3, 5]]
check = [False] * 3
m = sys.maxsize
def backtracking(row, score):
global m
if row == 3:
m = min(m, score)
return
for i in range(3):
if not check[i]:
check[i] = True
backtracking(row + 1, score + li[row][i])
check[i] = False
backtracking(0, 0)
print(m) # 8
N-Queen 문제
- BOJ N-Queen 참고
- N과 N의 각 행과 열에 N개의 퀸을 배치해야하기 때문에,
- (0, 0)부터 먼저 한개 배치
- 이때, 0번째 행, 0번째 열, 그리고
y = -x의 형태를 따라가는 대각선은 퀸을 놓을 수 없음 - 그럼, 그 다음 위치에 마찬가지로 퀸 한개를 더 배치
- (1, 2)에 배치한 이후, 위의 과정을 반복
- 위의 알고리즘을 재귀적으로 호출하며, 모든 N개의 퀸을 배치할 수 있다면
count + 1을 시행,- 하지만 배치가 불가능하다면, (0, 0)의 경우는 제외하고 (0, 1) 배치 시작
- 이때, 0번째 행, 0번째 열, 그리고
Code
N = int(input())
col_check = [False]*N
diagonal_check1 = [False]*(2*N-1)
diagonal_check2 = [False]*(2*N-1)
count = 0
def func(r):
global count
if r == N:
count += 1
return
for i in range(N):
if col_check[i] or diagonal_check1[i + r] or diagonal_check2[N - 1 - i + r]:
continue
col_check[i] = True
diagonal_check1[i + r] = True
diagonal_check2[N - 1 - i + r] = True
func(r + 1)
col_check[i] = False
diagonal_check1[i + r] = False
diagonal_check2[N - 1 - i + r] = False
func(0)
print(count)
- 참고 자료
2025.07.16
Selection Sort, Insertion Sort, Bubble Sort
- 선택 정렬이란,
- 비교 기반 정렬로써, 원소들을 서로 비교하면서 정렬을 수행
- 제자리 정렬이라는 특징을 갖음
- 추가적인 메모리 공간을 필요로 하지 않는다
- 불안정 정렬
- 👍 Pros
- 구현이 매우 간단
- 제자리 정렬
- 추가적인 메모리 공간을 요하지 않음
- 교환 횟수가 최소
- 👎 Cons
- 느린 수행 시간
- 불안정 정렬
- 입력의 상태와 관계 없는 수행 시간
Code
def selection_sort(num_list):
for i in range(len(num_list)):
min_index = i
for j in range(i + 1, len(num_list)):
if num_list[j] < num_list[min_index]:
min_index = j
num_list[i], num_list[min_index] = num_list[min_index], num_list[i]
return num_list
- 시 / 공간 복잡도
- 시간 복잡도의 경우, 최악, 평균 모두
O(n^2)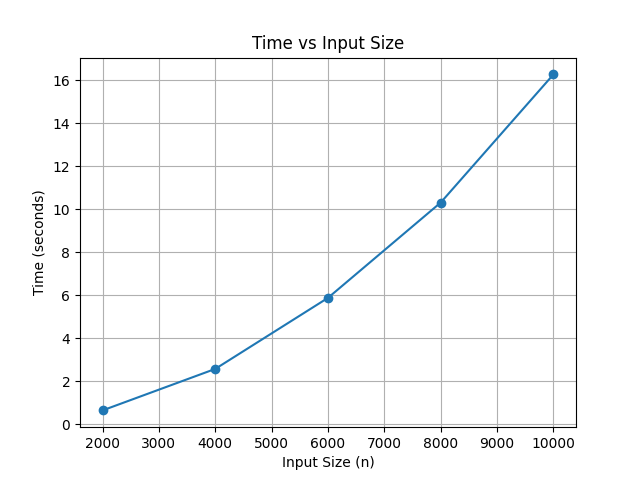
- 공간 복잡도의 경우,
O(1)- 제자리 정렬이기 때문
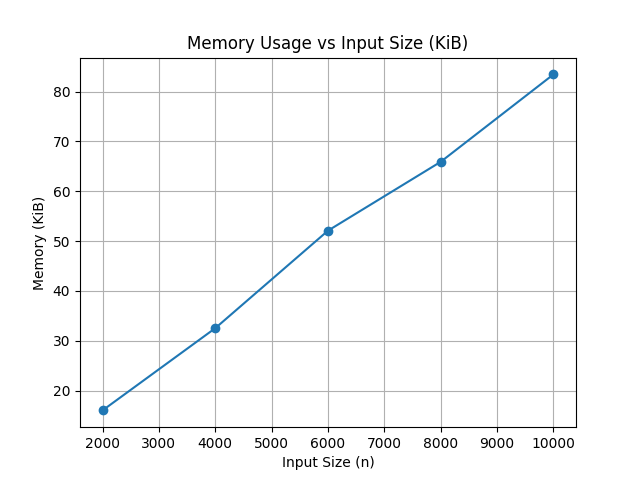
- 제자리 정렬이기 때문
- 시간 복잡도의 경우, 최악, 평균 모두
- 삽입 정렬이란,
- 비교 기반 정렬 알고리즘
- 인접한 원소들과 비교하며 정렬을 수행
- 때문에 데이터의 대부분이 정렬되어 있는 경우 효율적인 방식
- 제자리 정렬
- 추가적인 메모리 사용 없이 배열 내에서 처리
- 안정 정렬
- 동일한 값에 대하여 상대적 순서가 유지됨
- 입력 상태에서 성능이 달라짐
- 비교 기반 정렬 알고리즘
- 👍 Pros
- 구현이 간단하고 직관적
- 거의 정렬된 데이터에 대하여 매우 효율적
O(1)
- 안정 정렬이면서 제자리 정렬
- 👎 Cons
- 최악의 경우 성능이 매우 느림
- 대규모 데이터에 대해서는 적합하지 않은 선택
- 항상 많은 이동 연산이 발생할 수 있음
Code
def insertion_sort(num_list):
for i in range(1, len(num_list)):
key = num_list[i]
j = i - 1
while j >= 0 and num_list[j] > key:
num_list[j + 1] = num_list[j]
j -= 1
num_list[j + 1] = key
return num_list
- 시 / 공간 복잡도
- 최선의 경우
O(n), 최악의 경우 느린O(n^2)
- 최선의 경우, 아래의 그래프 (이미 정렬된 데이터라는 가정 하에 진행)
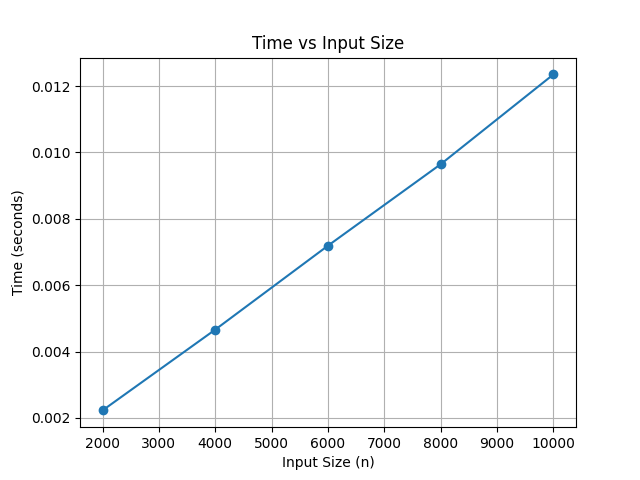
- 공간 복잡도
- 제자리 정렬이기 때문에
O(1)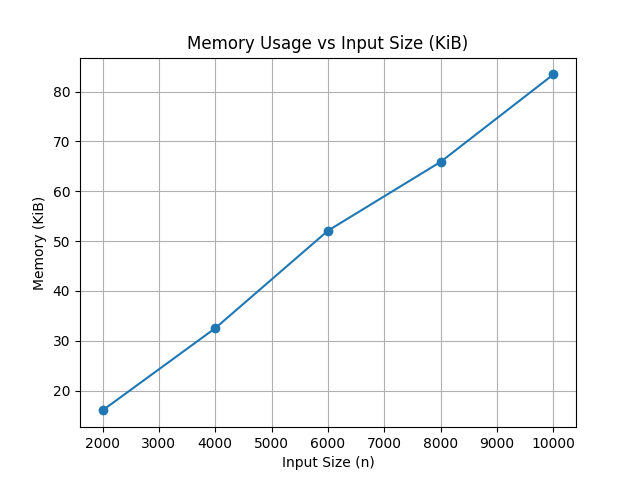
- 제자리 정렬이기 때문에
- 최선의 경우
- 버블 정렬이란,
- 가장 단순한 비교 기반 알고리즘
- 인접한 두 원소를 비교하는 방식
- 제자리 정렬이며 안정 정렬
- 👍 Pros
- 구현이 매우 간단하고 직관적
- 안정 정렬
- 작은 데이터셋에 유용
- 👎 Cons
- 느린 시간 복잡도
- 비교 횟수가 많음
- 사실상 거의 사용되지 않는 알고리즘 중 하나
- 시 / 공간 복잡도
- 시간 복잡도 :
O(n^2)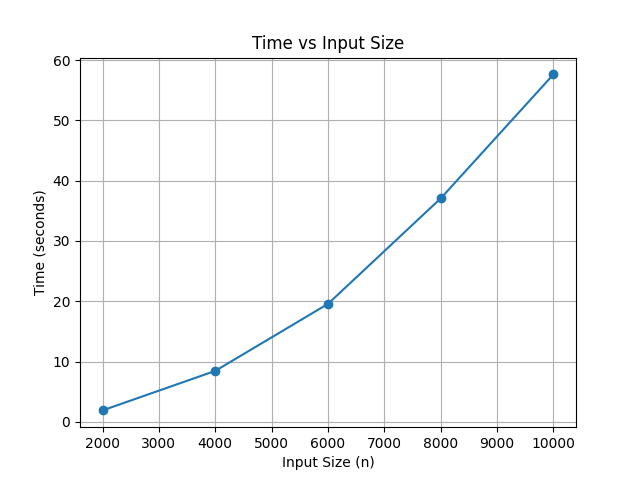
- 공간 복잡도 :
O(1)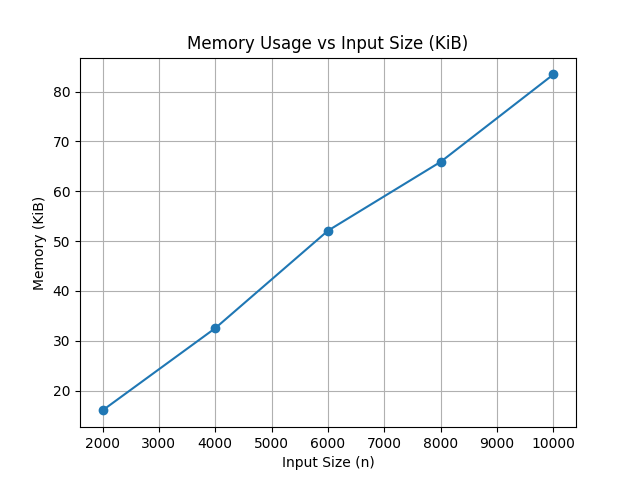
- 시간 복잡도 :